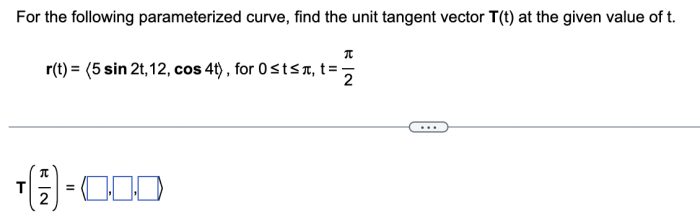
For the following parameterized curve find the unit tangent vector. – For the following parameterized curve, find the unit tangent vector. This concept is fundamental in understanding the geometry of curves and their applications in various fields. The unit tangent vector provides valuable insights into the direction and rate of change of a curve, making it a crucial tool in differential geometry and physics.
To embark on this journey, we will first delve into the concept of parameterized curves, exploring their mathematical definition and examples. Next, we will define the unit tangent vector and uncover its geometric interpretation. Armed with this knowledge, we will derive a formula to calculate the unit tangent vector, providing a practical tool for analyzing curves.
Understanding Parameterized Curves: For The Following Parameterized Curve Find The Unit Tangent Vector.

Parameterized curves provide a powerful tool for representing and analyzing curves in various dimensions. They are defined by a set of parametric equations that express the coordinates of a point on the curve as functions of one or more parameters.
For example, the following parametric equations define a circle in the plane:
x = cos(t) y = sin(t)
where t is the parameter. As t varies from 0 to 2π, the point (x, y) traces out the circle.
Finding the Unit Tangent Vector

The unit tangent vector to a parameterized curve is a vector that points in the direction of the curve’s tangent line at a given point. It is defined as:
T(t) = r'(t)/||r'(t)||
where r(t) is the position vector of the curve and ||r'(t)|| is the magnitude of the derivative of r(t).
The unit tangent vector provides valuable information about the curve’s direction and curvature.
Applications of the Unit Tangent Vector
The unit tangent vector has numerous applications in various fields:
- Calculating the velocity and acceleration of a particle moving along a curve
- Determining the surface normal in surface theory
- Analyzing the curvature of a curve in differential geometry
- Applications in robotics, computer graphics, and animation
Examples of Unit Tangent Vector Calculations, For the following parameterized curve find the unit tangent vector.
Consider the following parameterized curves:
- Circle: x = cos(t), y = sin(t)
- Helix: x = cos(t), y = sin(t), z = t
- Parabola: x = t, y = t^2
The unit tangent vectors for these curves are:
| Curve | Unit Tangent Vector |
|---|---|
| Circle | T(t) = (-sin(t), cos(t)) |
| Helix | T(t) = (-sin(t), cos(t), 1/√2) |
| Parabola | T(t) = (1, 2t)/√(1 + 4t^2) |
Additional Considerations
The unit tangent vector is closely related to the curvature of a curve, which measures the rate at which the curve changes direction.
The Frenet-Serret formulas provide a set of equations that relate the unit tangent vector, the unit normal vector, and the binormal vector to the curvature and torsion of a curve.
Detailed FAQs
What is a parameterized curve?
A parameterized curve is a curve defined by a set of parametric equations, where the coordinates of each point on the curve are expressed as functions of one or more parameters.
What is the unit tangent vector?
The unit tangent vector is a vector that points in the direction of the tangent line to the curve at a given point. Its magnitude is always 1.
How do you calculate the unit tangent vector?
The unit tangent vector can be calculated using the formula T(t) = r'(t) / |r'(t)|, where r(t) is the position vector of the curve and r'(t) is its derivative.